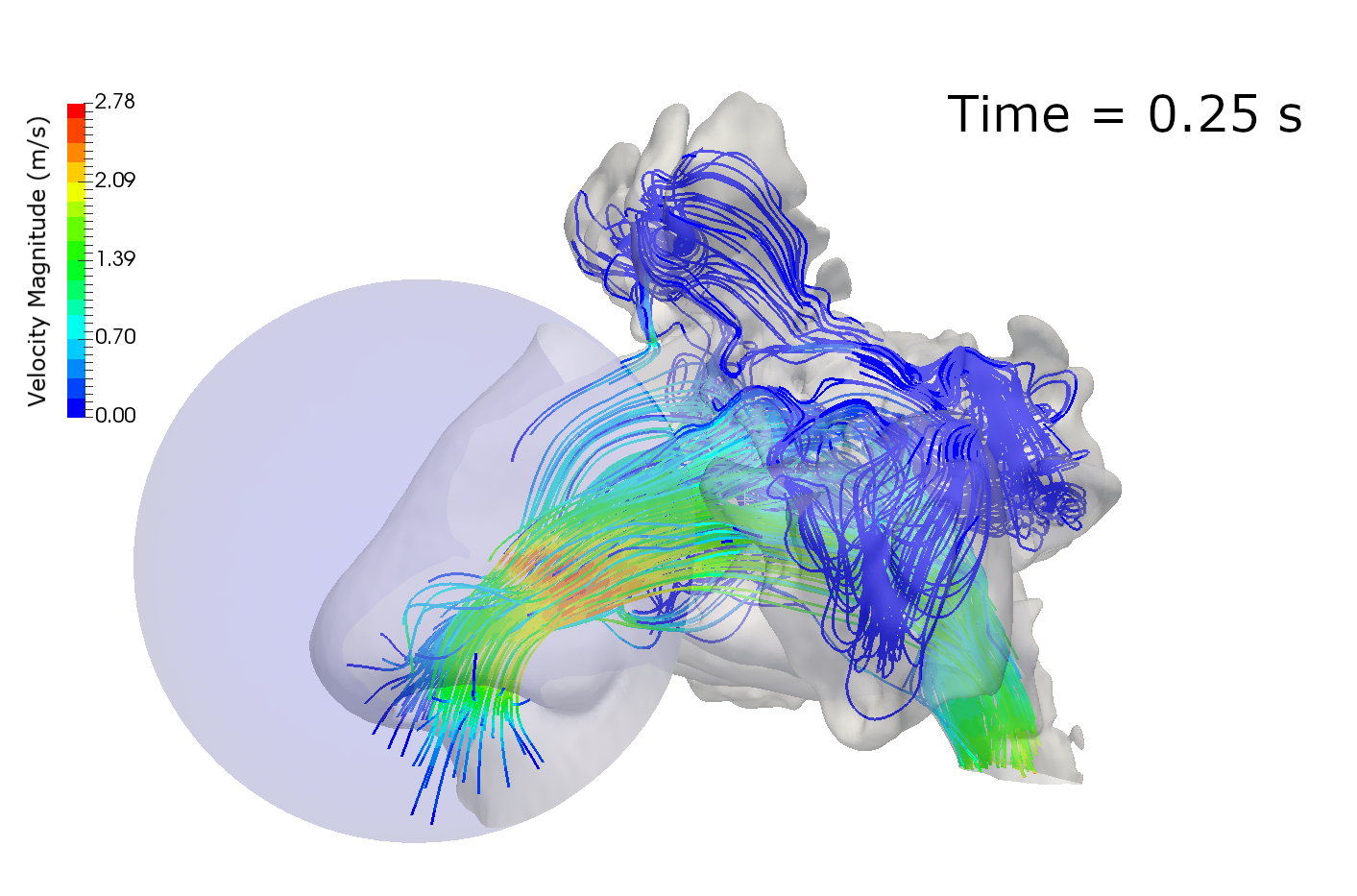
Numerical Modelling in Computational Continuum Mechanics
The age of conventional CFD methods, unstructured polyhedral meshes and Algebraic Multigrid (AMG) solvers is coming to an end. The future is best described in the AIAA CFD 2030 study, which demands much more: this is the focus of the research group. The work covers important areas of practically usable continuum mechanics simulation tools for the next 3 decades, keeping in mind the need for High-Performance Computing (HPC) support across the board.
-
Complex geometry handling, such as next-generation Immersed Boundary Method, scalable Overset Mesh and dynamically refined multi-adaptive polyhedral meshes with dynamic load balancing on tens of thousands compute cores cores
-
Discontinuous Galerkin (DG) discretisation of arbitrary order with implicit discretisation methods, HPC support and h-p adaptivity
-
Conventional second-order FVM, extended to answer the needs of next-generation of users: time-spectral harmonic balance methods, non-conformal mesh interfaces originating in turbomachinery, extended for general use, Finite Area Method on curved surfaces and others
-
Special problems - usually PDEs higher than second-order, hyperbolic or non-conservative equations - require special discretisation practices. An example of recent work involves polyhedral non-conservative discretisation for aero-thermo-acoustic problems
-
Solution of strongly coupled equation sets such as neutronics equations, strongly coupled chemical reaction sets or block-implicit pressure-velocity matrices offer substantial challenges. They are studied in detail: in our research we provide customised solution methods, sometimes 100s or 1000s of times faster than conventional segregated solution techniques.
This numerics basis, together with our work on HPC Linear Algebra is the basis for model development in Complex Physics. We focus on continuum models with significant non-linearity and inter-equation coupling: turbulent fluid flow is only a sample starting point
